Rope around the World

by R. Grothmnann

This notebook contains some interesting computations on the surface of a large ball, e.g. the earth. These computations face serious numerical problems. We discuss methods to overcome these problems.

The radius of the Earth is stored in one of the unit variables of Euler.

>r=rEarth$

The first task is to make the perimeter of the earth 1m longer. How much would the radius change?

The answer does not depend on the radius, and is very simple.

>1/(2*pi)

0.159154943092

Next, we ask, how much the radius would have to change, so that the surface increases by 1m^2.

The formula for the surface is 4*pi*r^2. We can find a good solution by using the derivative of this.

>longformat; 1/(8*pi*r)

6.25928709709e-009

The answer is in the Nanometer range!

Of course, we can also compute this exactly, or at least, we can try. We use Maxima for this.

>function O(r) &= 4*%pi*r^2, &expand(O(r+x)-O(r)=1), sol &= solve(%,x)

                                     2
                               4 pi r


                              2
                        4 pi x  + 8 pi r x = 1


                                  2
            - sqrt(pi) sqrt(4 pi r  + 1) - 2 pi r
       [x = -------------------------------------, 
                            2 pi
                                                      2
                                  sqrt(pi) sqrt(4 pi r  + 1) - 2 pi r
                              x = -----------------------------------]
                                                 2 pi

If we evaluate the solutions, we get a very larger error for the second solution, which is the one we are interested in.

>sol()

[-12713504,  7.11478038543e-009]

We could use Maxima to compute with more digits.

>fpprec&:=30; &bfloat(rhs(sol[2])) with r=@r

                  6.25928709708571598860444074691b-9

We get the same solution as with the simple differentiation method above.

There is another trick: We can compute the other solution, and remember that the product of the solutins must be 1.

>1/(-4*pi*&rhs(sol[1])())

6.25928709709e-009

And, in Euler, we can use the interval Newton method to get a very good solution of our problem, which even is a guaranteed inclusion!

>&expand(O(x+r)-O(r)-1), mxminewton(%,~0,1~)

                              2
                        4 pi x  + 8 pi r x - 1

~6.2592870970857117e-009,6.25928709708572e-009~

In the next problem, we put a rope around the earth, which is 1m longer than the perimeter, and pull it up at one point as much as possible.

With a little geometry we get a formula describing the situation. However, it turns out to be very unstable.

>f="sqrt(2*x*r+x^2)-acos(r/(r+x))*r-0.5";

However, we can find a solution with the bisection method.

>longformat; bisect(f,100,200)

121.370109635

Likewise, with the secant method.

>longformat; secant(f,100,200)

121.370113117

Nothing seems wrong.

However, if we plot the formula, we see that something strange is happening.

>plot2d(f,a=121.4382,b=121.4383,adaptive=0):

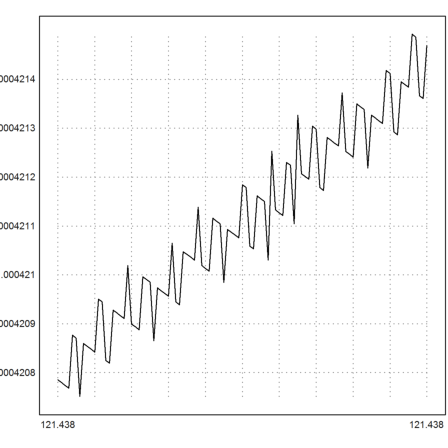
Rope around the World

Let us try another method. We solve for the angle of the chord, along which the rope is lifted.

>a=bisect("tan(x)-x-0.5/r",0,1)

0.00617944947498

The height can be computed from this.

>(1/cos(a)-1)*r

121.370112359

A short computation shows, that the rope is in the air for about 79km.

>2*a*r

78562.455618

Again, the interval Newton method leads to a very good inclusion.

>a=inewton("tan(x)-x-0.5/r","tan(x)^2",~0.006,0.007~)

~0.006179449475557,0.006179449475647~

However, we have to evaluate the derivative carefully, since it is close to 0. The simple derivarive 1/cos(x)^2-1 as returned by Maxima easily contains 0, if evaluated with interval arithmetic.

>mxmieval("::diff(tan(x)-x,x)",~0.001,0.01~)

~9.95e-007,0.000101~

Only if we start really close to the solution, we get an automatic inclusion.

>mxminewton("tan(x)-x-0.5/r",~0.006,0.007~)

~0.006179449475553,0.006179449475643~

Let us compute the height.

>(1/cos(a)-1)*r

~121.370112378,121.370112388~

The next task is to increment the surface by 1m^2 by pulling out at a point.

With some geometry we get the equation cos(a)+1/cos(a)=2+1/(pi*r^2) for the angle a. However, this is again a very unstable equation.

>2+1/(pi*r^2)

Let us solve in Maxima.

>:: expr := cos(a)+1/cos(a)=2+1/(%pi*r^2), sol := solve(%,cos(a))

                                1        1
                     cos(a) + ------ = ----- + 2
                              cos(a)       2
                                       pi r


                              2              2
                   sqrt(4 pi r  + 1) - 2 pi r  - 1
       [cos(a) = - -------------------------------, 
                                     2
                               2 pi r
                                                 2              2
                                      sqrt(4 pi r  + 1) + 2 pi r  + 1
                             cos(a) = -------------------------------]
                                                        2
                                                  2 pi r

Now Euler can compute the angle.

>acos(mxmeval("rhs(sol[1])"))

0.000421317878792

It is far easier to approximat cos(a)=1-a^2/2 and solve for a. We get the same result.

>a=(4/(pi*r^2))^(1/4)

0.000421317885102

This formula is derived by developping the right hand side for a at 1.

>:: taylor((1-a^2/2) + 1/(1-a^2/2),a,0,4)

                                 4
                                a
      /T/                   2 + -- + . . .
                                4

The height we can lift our surface is about 56cm.

>(1/cos(a)-1)*r

0.564189625348

Examples